АЛГЕБРА И ЛОГИКА: CТАРЫЕ И НОВЫЕ СВЯЗИ*

Ю.Л. Ершов

* Научное сообщение академика Ю.Л.Ершова на заседании Президиума РАН (Москва, 12 ноября 2003 г.). Текст подготовлен на основе стенограммы заседания.

Я благодарен за предоставленную мне возможность выступить здесь с докладом, хотя задача моя не из легких, поскольку то, о чем хочу рассказать, относится к наиболее абстрактным частям математики, которая сама по себе является одной из самых абстрактных наук. Алгебра и логика – это довольно широкие области исследования, и там ведется активная и плодотворная работа. Я выбрал узкое направление их взаимодействия, направление, которое, на мой взгляд, представляет интерес. И рассмотрев его в исторической перспективе, я постараюсь удержать внимание уважаемого научного сообщества как можно дольше, потому что рассказывать совсем технические результаты достаточно сложно.

Итак, алгебра и логика, их старые и новые связи. Слова «алгебра» и «логика» всем знакомы. Алгебра знакома из школьного курса, а насчет логики уместно рассказать такую быль. Один мой остроумный коллега рассказал о недавнем разговоре с другим своим коллегой-математиком. Он сказал: «Я занимаюсь математической логикой» – и тот вполне искренне ответил следующее: «Ты знаешь, а я в своей деятельности логикой никогда не пользовался!». Должен сказать, что это почище литературного героя, который был поражен, когда узнал, что говорит прозой. И это сказал математик!

Взаимодействия между математикой и логикой достаточно интересны. Я выделил в этих взаимодействиях три исторических периода. Они не взаимоисключающие, они пересекаются, когда, образно говоря, алгебра выполняет по совместительству роль математической логики и теории алгоритмов.

Что значит «выполняет роль» и какова роль математической логики? Взгляд на исторические периоды ретроспективный, – с нынешней точки зрения мы можем интерпретировать события, которые имели место в прошлом.

Математика знаменита тем, что в ней созданы и опробованы все логические методы. Это одно из тех средств, с помощью которого математика достигла и достигает в настоящее время своего высокого уровня строгости. Известно, что пик «совершенства» в «доисторический» период – аксиоматическое представление геометрии Евклидом. Суть его состоит в следующем: изложение научной дисциплины, например геометрии, начинается с точной формулировки аксиом – «первоначальных истин», а все остальное, т.е. последовательное изложение, получается логическим выведением всех остальных теорем из принятых предпосылок.

Действительно, аксиоматический метод сыграл и играет важную роль не только в математике, но и в других дисциплинах. Но я бы сказал, что с логикой у Евклида было слабовато. В каком смысле? Дело в том, что он относился к логике как к чему-то само собой разумеющемуся. Это достаточно прагматичная точка зрения. Не скажу, что она такая уж плохая: на протяжении многих веков она если и мешала, то несильно. Иногда даже известные ученые делали элементарные логические ошибки. Это было еще терпимо, но на рубеже XIX–XX вв. возникли так называемые парадоксы, которые поставили под сомнение роль математики как наиболее точной и безупречной науки. Парадокс – это когда одни и те же рассуждения, которые принимаются научным сообществом, приводят в одном случае к одному результату, в другом – к противоположному. Тогда осознали необходимость сделать еще один шаг в развитии аксиоматического метода: нужно точно выявить те логические средства, которые разрешается использовать для получения следствий, для их выведения.

Это и было проблемой, которая на рубеже XIX–XX вв. привела к созданию математической логики. Тем не менее в течение веков алгебра, которая является одной из древнейших математических наук, на самом деле демонстрировала примеры точных, в том числе и формальных, логических преобразований, но не на уровне самых сложных логических утверждений, а на уровне тождеств. Можно сказать, что алгебра кодифицировала работу с тождествами. Это довольно важный момент. И сейчас я обращусь к простому примеру из школьной алгебры. В школе изучают решение уравнения x2 + ax + b, где a и b – параметры решения, и нужно найти корни этого уравнения. Как это происходит? Делаются некоторые преобразования, и получается формула для решения, которая дает решение этого квадратного уравнения:

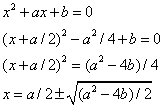
Эти тождественные преобразования приводят к решению задач, в частности к нахождению корней уравнения, а нахождение корней уравнения – это была задача, которую и теория чисел, и арифметика ставили, а алгебра пыталась решать эти уравнения в общем виде.

Другая точка зрения (когда уже получили это решение) состоит в следующем. Эта формула на самом деле представляет собой запись некоторого алгоритма нахождения решения. Ее можно интерпретировать как некоторые указания: что нужно сделать, какие арифметические операции нужно произвести с коэффициентами, для того чтобы найти корень квадратного уравнения. То есть алгебраические формулы являли собой первые формальные записи алгоритмов. Поэтому алгебра выполняла роль и теории алгоритмов.

Одной из важнейших задач ХV–ХVI вв. была задача нахождения корней уравнений более высоких степеней. Например, известна формула Кардано для корня кубического уравнения:

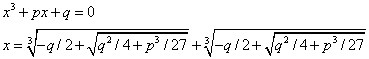
Здесь отсутствует квадрат в канонической записи уравнения, однако с помощью некоторых преобразований общее уравнение приводится к данному виду. Поэтому хотя это и более сложное выражение, но оно тоже представляет собой запись алгоритма для нахождения корней уравнений.

Итак, первый исторический период – VIII–XVI вв. Алгебра выполняет (по совместительству) роль (математической) логики и теории алгоритмов. Я приведу некоторые имена, которые относятся к этому периоду: Абу Джафар Мухаммад ибн Муса аль-Хорезми (787–850), Джелорамо Кардано (1501–1576), Лудовико Феррари (1522–1565), Франсуа Виет (1540–1603), Рене Декарт (1596–1650), Эварист Галуа (1811–1832) и др.

Первым я указал имя аль-Хорезми, который не так хорошо известен широкой общественности, но тем не менее это человек уникальный. Он родился в конце VII в. и прожил до середины VIII в. Два слова, которые в математическом обиходе и даже в общечеловеческом обиходе сейчас присутствуют, – слова «алгоритм» и «алгебра» связаны с именем этого человека.

Слово «алгоритм» – это трансформация имени аль-Хорезми (по латыни dixit algorizmi – так сказал аль-Хорезми), а слово «алгебра» возникло из части арабского названия его книги по алгебре «Китат аль-мухассар ибн хасаб аль-габр д’алуккабала». Это уникальный случай, когда два таких важнейших и широких понятия связаны с именем одного человека, причем жил он достаточно давно.

Следом идут имена тех итальянцев, которые искали, пытались найти общие формулы для решения уравнений от одной переменной более высоких степеней.

Принципиальный шаг, который был сделан далее, связан с именем выдающегося французского философа Рене Декарта. В данном контексте упомянуть его имя важно потому, что, введя координаты, Декарт впервые показал, что многие геометрические вопросы можно сформулировать алгебраически, т.е. опять же свести к вопросам решения уравнений, систем уравнений и т.д.

Известны слова Сальери из трагедии Пушкина «Моцарт и Сальери»: «…Поверил я алгеброй гармонию». Эти слова показывают, что Пушкин интуитивно понимал, что с алгеброй связан некоторый формальный подход, который позволяет анализировать. Так вот, я бы сказал, что Рене Декарт поверил алгеброй геометрию. И это было действительно выдающимся достижением. А то, что алгебра создала технику преобразования уравнений и решения уравнений, – тому есть такое внешнее свидетельство: недавно появился перевод довольно серьезной книги американского философа Рэндала Коллинза «Социология философии. Глобальная теория интеллектуального изменения», где он анализирует развитие науки, и в частности говорит, что развитие науки в Европе, расцвет науки ХVI–XVII вв. связан с введением новых приборов. Появление этих приборов стимулировало «науку быстрых открытий». Математика становится машиной по производству открытий. И Декарт «был воинственным защитником нового алгебраического подхода, он освобождал последнюю из областей математики, оставшихся неосвобожденными от гуманистического возрождения классики, и превращал их в техники быстрого решения задач». В то же время Коллинз говорит, что другим источником «теории быстрых открытий» была математика, в частности алгебра как наука, которая доставляла технику решения и преобразований. На самом деле алгебра являлась аналогом приборной базы современной науки.

Наконец, Эварист Галуа, трагически погибший молодым гениальный французский математик, который доказал, что для уравнения пятой степени общей формулы не существует. Это было замечательным достижением. Причем это было замечательным достижением и с точки зрения средств, которыми было получено доказательство, потому что аналогичный результат показал и Абель, но Галуа это сделал таким способом, что я называю его предвестником или одним из основателей современной математики. Он для решения задач классической математики привлек к изучению другие, новые объекты: группы автоморфизмов, конечные группы, конечные поля и т.д. С другой стороны, сам результат Галуа можно интерпретировать и с алгоритмической точки зрения. Можно сказать, что теорема Галуа является первым примером алгоритмически неразрешимой проблемы. Если понимать под алгоритмом формулу, которая выражает корень через радикалы, сложение, умножение и деление, то он показал, что такого представления, такого алгоритма просто не существует. Потом понятие «алгоритм» приобрело более общую форму.

Второй исторический период – XVII–XX вв. Алгебра помогает логике найти свой путь в математике. Здесь тоже можно привести целый ряд имен: Готфрид Лейбниц (1646–1716), Джордж Буль (1815–1864), Эрнст Шредер (1841–1902), Готлоб Фреге (1848–1925), Давид Гильберт (1862–1943) и др.

Выдающийся немецкий философ Готфрид Лейбниц по праву может считаться основателем математической логики. Он первым в явном виде поставил задачу и попытался ввести универсальный язык, универсальное исчисление, которое могло бы охватывать всю математику. Кроме того, наряду с Ньютоном он был создателем математического анализа. Но он был и основателем математической логики, так как первым осознал необходимость этого. Второй элемент, который математическая логика внесла в усовершенствование аксиоматического метода, и в этом отношении алгебра серьезно помогла, – это использование все более богатых формальных языков. Сам успех в технологии решения во многом был связан с введением формальных языков и точных правил их преобразования. Если алгебра работала с тождествами, с преобразованиями тождеств, то Лейбниц поставил задачу о том, нельзя ли создать такой формальный язык, который позволяет точно говорить обо всем (вычислять).

Далее, такие математики, как Буль и Шредер, попытались первыми более успешно решить эту задачу. Потому нельзя сказать, что Лейбниц успешно решил задачу создания универсального формального языка. Попытку формализовать логику одним из первых предпринял английский математик Буль, имя которого в математике осталось в названии «булевы алгебры». Это показывает, что алгебра была той путеводной звездой, которая в конце концов привела к построению современной математической логики.

Еще одно имя – Давид Гильберт, которого я указал как заключительную ключевую фигуру второго периода. Это выдающийся немецкий математик, который работал во многих областях математики, в частности в теории чисел, в математической физике и др., и сыграл большую роль в создании и формализации математической логики. Он в некотором смысле завершил второй цикл. На рубеже XIX–XX вв. он опубликовал книгу «Основания геометрии». Это было современное аксиоматическое изложение геометрии где наряду с геометрическими аксиомами были в явном виде сформулированы и логические аксиомы, т.е. в явном виде указаны те логические средства, которые допустимы для получения результатов и для доказательства теорем.

На основе этого произошло много разных событий. В частности, когда в явном виде формализуются некоторые аксиомы, то возникают совершенно неожиданные вещи. Когда была аксиоматизирована теория множеств и была в явном виде сформулирована аксиома выбора, которой интуитивно и неявно пользовались многие математики, сразу обнаружилось, что она ведет к парадоксальным следствиям. А выявление логических средств, скажем рассуждения от противного, привело к тому, что сам Гильберт в своей деятельности стал пользоваться этим. Он нашел довольно короткое доказательство знаменитой теоремы о конечности инвариантов, используя рассуждения от противного. Как следствие, наблюдалось некоторое отторжение предложенного Гильбертом доказательства со стороны математиков, которые занимались этой проблемой, поскольку классическая математика была интуитивно конструктивной. То есть когда говорится о чем-то, что существует, то должен быть указан путь построения этого объекта, а не только доказательство его существования. Тем не менее для получения знаний и рассуждения от противного являются ничуть не худшим средством.

Итак, на рубеже XIX–XX вв. математическая логика как самостоятельная дисциплина была сформирована, но не все задачи она решила. Одной из целей Гильберта было построить такое формальное исчисление, в которое укладывается вся математика, и доказать его непротиворечивость, т.е. на все времена обеспечить себе благополучное будущее. Эта цель не была достигнута из-за теорем Геделя, хотя это и не является совершенно неожиданным. Тем не менее цель по достижению большей точности в математике была достигнута (в виде развития аксиоматического метода в вышеозначенных двух шагах).

Казалось бы, математическая логика выполнила свою роль, но наступил третий период – на самом деле уникальный период, когда логика начинает «отдавать долги» алгебре. И произошло это, на мой взгляд, совершенно неожиданно. Исторически это ничем не было оправдано. В 1941 г. Анатолий Иванович Мальцев, тогда еще не академик, опубликовал статью, которая называлась «Об одном общем методе получения локальных теорем в теории групп».

Некоторая предыстория: в 1936 г. Анатолий Иванович доказал очень важную теорему, относящуюся к математической логике, – так называемую теорему компактности языка исчисления предикатов, которая послужила основой для создания целого раздела математической логики, носящего название «теория моделей» и вполне успешно развивающегося в настоящее время. Он обнаружил, что некоторые теоремы из теории групп, каждая из которых имела свое собственное, часто довольно сложное доказательство, которые носят название локальных теорем, на самом деле суть следствия общего принципа математической логики, причем куда более простые следствия теоремы компактности, чем их конкретные доказательства.

Несколько слов по поводу того, что же это такое – локальная теорема. Я приведу один конкретный пример и надеюсь, что этот пример не только математики, но и физики могут понять.

Что такое группа? Я уже упомянул о группах в связи с именем Галуа, группа – это такая алгебраическая система, которая описывает симметрии или автоморфизмы, если говорить математическим языком. В частности, если есть n-мерное векторное пространство над комплексными числами, то его группа автоморфизмов – так называемая общая линейная группа – очень конструктивна. Если зафиксировать базис этого векторного пространства, каждый автоморфизм описывается квадратной матрицей порядка n ´ n, а умножение этих автоморфизмов на самом деле есть умножение матриц. Поэтому это вполне конкретный объект, в котором можно считать.

И вопрос о том, имеет ли какая-то группа, которая возникла, быть может, из совсем других соображений, матричное представление (есть ли изоморфное вложение этой группы в группу матриц), часто очень важен. Так вот, одна из локальных теорем говорит следующее: если группа такова, что каждая подгруппа, которая порождается конечным числом элементов, имеет изоморфное вложение в группу матриц порядка n ´ n, то и сама группа имеет изоморфное вложение в группу матриц порядка n ´ n. Так, свойство иметь точное матричное представление на самом деле является локальным свойством: если есть какое-то препятствие вложению, то это препятствие на самом деле реализуется на какой-то конечной порожденной подгруппе. Таких теорем – море. Алгебраическое доказательство этой теоремы довольно сложное, а логическое – простое.

С появлением этой работы наступил третий этап, который успешно продолжается до настоящего времени. Итак, третий исторический период – с 1941 г. по настоящее время. Логика начинает «отдавать долги» алгебре. Имена, которые здесь надо назвать, – Анатолий Иванович Мальцев (1909–1967), Альфред Тарский (1902–1983), Абрахам Робинсон (1918–1974), Ян Денеф, Ехуд Хрущовский и др.

Альфред Тарский и Абрахам Робинсон – это математики, которые наряду с Анатолием Ивановичем Мальцевым являются создателями раздела математической логики, называемого теорией моделей. Теория моделей оказалась весьма успешной. Но меня интересуют взаимоотношения логики и алгебры с другими разделами математики. Альфред Тарский с помощью математической логики обосновал так называемый принцип Лефшеца. Известный американский тополог и алгебраический геометр Соломон Лефшец (1884–1972) сформулировал такой неформальный принцип: если что-то в алгебраической геометрии доказано над полем комплексных чисел, то это справедливо и для любого алгебраически замкнутого поля. Оказывается, что если переформулировать это логически, то можно и доказать.

Абрахам Робинсон, который ввел довольно много полезных понятий в теорию моделей, предложил математическую модель понятия бесконечно малого. Тот жe Лейбниц при построении анализа пользовался понятием бесконечно малого, которое потом было изгнано при современном изложении анализа. Можно было обойтись без бесконечно малых, тем не менее это имело свой эвристический смысл. Оказывается, что на самом деле можно построить такие модели чисел, в которых есть бесконечно малые, и ими можно пользоваться.

Третий этап – это применение математической логики в современной алгебре, применение в современной математике.

Оказывается, однако, что методы математической логики могут успешно применяться и к классическим объектам, связанным с арифметикой, теорией чисел, алгебраической геометрией. Так, бельгийский математик Ян Денеф дал логическое доказательство гипотезы Шафаревича – Боревича о рациональности рядов Вейля, связанных с числом точек решения уравнений по модулю pn. Не буду вдаваться в подробности, но сам факт важен. Впервые эту гипотезу алгебро-геометрическими методами доказал Джи Игуза, а Денеф, используя то, что логика p-адических чисел хорошо известна, дал другое доказательство – более простое и логическое.

Израильский математик Ехуд Хрущовский решил некоторые трудные арифметико-алгебраические проблемы, связанные с числом точек абелевых многообразий, – это гипотеза Мамфорда, гипотеза Манина и т.д. Здесь ситуация такова: было найдено логическое доказательство для гипотез, для которых нелогических доказательств просто не было.

В заключение хочу кое-что пояснить в связи с некоторыми моими работами. Классическая математика рассматривает ограничения числа объектов – рациональные, вещественные и комплексные числа, плоскости, пространства и проч. Современная же математика не ограничивает себя выборе объектов и создает, если нужно, все новые и новые. Чтобы плодотворно работать в таком многообразии объектов, нужно уметь выбирать «наиболее важные» с той или иной точки зрения, которые позволяют пролить свет на ситуацию в целом. Так, традиционным подходом в математике является рассмотрение в первую очередь полных (метрических, топологических и др.) пространств вместе с процедурами пополнения. Теория категорий полезна тем, что подсказывает изучение проективных и инвективных объектов категории. Математическая логика вносит свой положительный вклад в создание методологии выбора «важных» объектов.

Объекты из таких важных понятий, ведущих происхождение из логики, является понятие E-замкнутой системы. Попробую пояснить на примере. Пусть C – поле комплексных чисел; F₀ £ F₁ – подполя C (т.е. подмножества, замкнутые относительно сложения, вычитания, умножения и деления на числа, отличные от нуля). F₀ является E-замкнутым в F₁ если любая конечная система равенств и неравенств многочленов над F₀, имеющая решение в F₁ имеет решение и в F₀. Если K – какой-либо класс подполей поля C, то поле F из K является E-замкнутым (в классе K), если для любого поля F₀ из K такого, что F £ F₀ (F подполе F₀), F является E-замкнутым в F₀. Варьируя класс K будем получать разные понятия. Так, если класс K состоит из всех подполей поля C, то E-замкнутыми в K будут в точности алгебраически замкнутые подполя поля C.

Вопрос о существовании E-замкнутых полей в классе K решается положительно, если K замкнут относительно объединения цепей вложенных друг в друга элементов из K.

Классический объект теории чисел – поле рациональных чисел Q имеет ряд естественных метрик: одна связана с естественным линейным порядком на Q, другая определяется с помощью отношения делимости в кольце целых чисел Z £ Q по степени фиксированного простого числа p. Пополнения Q по этим метрикам дают поле вещественных чисел и поля p-адических чисел. Все эти пополнения оказывались более «простыми» объектами. И математическая логика придала точный смысл этой «простоте», которая ранее ощущалась на прагматическом уровне – в них проще решать уравнения.

В 1948 году Альфред Тарский доказал алгоритмическую разрешимость для вещественных чисел, а в 1965 г. (как ответ на вопрос Тарского) алгоритмическая разрешимость поля p-адических чисел была показана мною и американскими математиками (вместе) – специалистом по теории чисел Дж. Аксом и специалистом по теории моделей С.Кочиным. Алгоритмическая разрешимость поля означает существование алгоритма, который на любой вопрос о справедливости того или иного утверждения для поля дает (правильный) ответ, справедливо оно или нет. Заметим, что для поля рациональных чисел Q такого алгоритма не может существовать.

Итак, было показано, что существует бесконечно много «хороших» пополнений поля Q. Меня заинтересовал вопрос: можно ли «собрать» эти (несравнимые между собой) пополнения в одно «хорошее» поле? Положительный ответ удалось получить, используя понятие E-замкнутого поля в подходящем классе полей. В 1936 г. французский математик К.Шевалье ввел в рассмотрение важное кольцо аделей (подходящее подкольцо прямого произведения полей вещественных и p-адических чисел), в терминах которых изящно изложил так называемую глобальную теорию полей классов – один из наиболее глубоких разделов теории чисел. Если в качестве класса K полей взять семейство всех счетных подполей кольца аделей, то E-замкнутые поля в K – это поля, которые я назвал удивительными расширениями поля рациональных чисел. Оказалось, что все такие поля имеют одну и ту же теорию (одни и те же свойства) и эта теория алгоритмически разрешима. Эта теория также «содержит» в себе равномерно все теории вещественных и p-адических чисел.

Впоследствии (cм. мою заметку в «Докладах РАН» за 2003 г.) оказалось, что эти удивительные расширения можно использовать и для нового представления глобальной теории полей классов. Поскольку теория удивительных расширений алгоритмически разрешима, постольку и саму глобальную теорию полей классов можно эффективизировать, в частности отображение взаимности можно равномерно вычислить.

Суммируя достижения третьего этапа, можно отметить, что использование методов математической логики продемонстрировало свою успешность начиная с решения проблем современной математики, далее, в решении проблем классической математики и, наконец, как «вмешательство» в понятийный аппарат классической математики. Нет сомнений и в дальнейшем прогрессе в «отдавании долгов».

Институт математики СО РАН

г. Новосибирск

Yershov, Yu.L. Algebra and logic: their old and new relations.

The paper considers interrelation and interaction of algebra and logic. It presents a historical perspective of this process and describes its modern achievements in solution of mathematical problems.