ФРАКТАЛЬНАЯ КОНЦЕПЦИЯ ДЕТЕРМИНИРОВАННОГО ХАОСА
Г.А. Донцов, Г.С. Мельников, И.Н. Серов
В последние годы в науке и философии широко
обсуждается проблема классификации и объяснения явлений детерминированного
хаоса. Эта проблема связывает такие науки, как астрономия,
радиофизика, физика твердого тела, биофизика, биология, химическая кинетика,
информатика, экономика, экология, медицина и др. [1]. В свою очередь,
открытие явлений детерминированного хаоса поставило новые вопросы, и прежде
всего вопрос о том, как теперь соотносятся категории "порядок" и
"хаос". Сейчас уже трудно представить хоть сколько-нибудь известную
нелинейную систему, в которой не найдены хаотические режимы.
В 1963 г. настоящей сенсацией, положившей начало
исследовательскому буму, стало открытие сложного поведения сравнительно простой
динамической системы, описывающей тепловую трехмодовую
конвекцию атмосферы. Это открытие случайно сделал в Массачусетском
технологическом институте Э.Лоренц, специалист по физике атмосферы [2].
Модельная система Лоренца была получена в результате некоторых упрощений из
уравнений Навье – Стокса и впоследствии изучалась в сотнях работ, став к
настоящему времени одной из самых известных моделей хаоса. Нерегулярные
колебания, наблюдаемые в модели Лоренца, и аналогичные им получили название
динамического, или детерминированного, хаоса. Динамическими, или
детерминированными, такие хаотические режимы были названы потому, что они
возникают в системах, описываемых обыкновенными динамическими уравнениями,
решение которых однозначно определено начальными условиями [3].
Динамический хаос [4]. Где лежит граница между регулярной, но сложноорганизованной
структурой, т.е. порядком, и беспорядком? Часто под беспорядком подразумевается
проявление системой качественно нового режима – хаоса. Критерием
возникновения такого режима может служить устойчивость возникающих в системе
образований по отношению к малым возмущениям. Если такая устойчивость
отсутствует, детерминированное описание теряет смысл и необходимо использовать
статистические методы.
Однако, как показали многочисленные исследования,
статистические законы, а вместе с ними и статистическое описание относятся не
только к очень сложным системам с большим числом степеней свободы. Дело здесь
не в сложности исследуемой системы и не во внешних шумах, а в появлении при
некоторых значениях параметров экспоненциальной неустойчивости движения.
Впервые эта концепция получила строгое обоснование на
простейшей модели статистической механики – бильярде. Хорошо известно, что
к системам, свойства которых отвечают свойствам бильярдов, сводится ряд задач
статистической физики. По существу, математический плоский
бильярд представляет собой обычный бильярд, только с произвольной конфигурацией
стола и без луз. Оказывается, что в зависимости от формы границы даже чисто
детерминированная система из двух шаров (!) может обладать свойством
хаотичности.
Какие же законы управляют хаосом? Возможно
ли создать математический аппарат, позволяющий непротиворечиво описывать
хаотическую динамику и предсказывать появление хаоса в тех или иных системах?
Наконец, можно ли найти методы предсказания поведения хаотических систем?
Ответами на эти и ряд других вопросов занимается теория динамического
(детерминированного) хаоса, являющаяся одним из разделов нелинейной динамики.
К настоящему времени разработаны методы классификации различных типов хаоса,
найдены закономерности его развития, созданы техники, позволяющие отличить
(например, в эксперименте) хаос от белого шума, и т.п. Более того, обнаружено и
строго обосновано, что сложное пространственно-временное поведение
распределенных сред с громадным числом степеней свободы может быть адекватно
описано нелинейными системами небольшой размерности.
Порядок [9] –
категория, означающая определенность пространственного или временного положения
элементов некоторого множества или системы, подразумевающая наличие устойчивых
связей между элементами, существование некоторого закона или симметрии, которым
подчиняются эти элементы, и возможность предсказания допустимых изменений.
Часто эта категория употребляется в более узком смысле, т.е. означает наличие
определенных количественных соотношений между размерами и формой частей
системы. Изменение связей между элементами может изменить порядок или разрушить
его. В человеческом сознании порядок противоположен хаосу. Долгое время понятие
"порядок" считалось синонимом понятия “закон”.
Термин “упорядоченный” означает «правильный,
определенный, предсказуемый». В физике он сначала обозначал существование
некоторых пространственных структур, – например, в кристаллофизике,
гидродинамике, атомной физике. В теории колебаний термин “упорядоченный” (или
“регулярный”) стал обозначать движения и состояния, развивающиеся по
определенному закону, обладающие определенными характеристиками и полностью
предсказуемые. В этом случае имеется в виду прежде
всего временной порядок, который влечет за собой порядок пространственных форм.
Фрактальность [6]. Фрактальная
геометрия не есть "чистая" геометрическая теория. Это скорее
концепция, новый взгляд на хорошо известные вещи, перестройка восприятия,
заставляющая исследователя по-новому видеть мир. Б.Мандельброт сделал сильный
методологический ход, перейдя к фракталу – предмету измерения
как математики, так и прикладных наук, сконструировав две процедуры
отождествления: процедуру отождествления рекурсивных математических
"монстров" как фракталов и процедуру отождествления предметов
измерения фрактальной концепции и предметов измерения теоретических конструктов
прикладных исследований (географии, лингвистики, материаловедения и др.). В
этом смысле он объединил в некое целое разрозненные нагромождения фактов и
моделей, создав (предустановив)
"фрактальную" гармонию – фрактальный порядок интерпретируемого
мира, точнее, запустив интерсубъективный механизм самодостраивания, самоорганизации этого порядка.
Если
попытаться понять, какую роль играют понятия, вводимые Мандельбротом, –
какие "языковые игры" они ведут, то можно заметить, что язык введения
категории фрактала не связан напрямую с уточнением и ограничением данного
понятия. Это впечатление усиливается и при прочтении его «Фрактальной геометрии
природы» [6]. Мандельброт вводит категорию фрактала фрактально, дает "затравку" – первые (пусть и неверные) определения,
а потом запускает механизмы их итерации, изменений и пытается описать то, что
при этом получается, какие интерпретации при этом появляются.
Это
становится очевидным при рассмотрении проблемы определения фрактала. Как
известно, точного определения фрактала до сих пор не предложено. С одной
стороны, все формулировки разрушались контрпримерами.
С другой стороны, определение для категории фрактала особо и не нужно после
того, как возникла интерсубъективная практика
научного применения категории.
Действительно,
видно, что фрактал – фигура Коха и фрактал – множество Мандельброта
суть разные типы фракталов. Но у них есть и общее – наличие рекурсивной
процедуры их генерации. Различия же состоят в том, что в первом случае мы имеем
дело с инвариантным относительно масштабных преобразований фракталом, а во
втором – можно говорить о ковариантности, т.е. о
нарушениях инвариантности при масштабных преобразованиях. Поэтому можно
считать, что фигура Коха – это инвариантный фрактал, а множество
Мандельброта – это ковариантный (или, если взять на вооружение термин
Тимофеева-Ресовского, ковариантно редуплицированный)
фрактал.
Исходя из этого можно ввести представление о двух
пониманиях самоподобия: жестком самоподобии
(ЖС) – самоподобии типа самоподобия
фигур Коха, связанном инвариантностью относительно масштабных преобразований, и
нежестком самоподобии (НС) – ковариантном самоподобии типа самоподобия
множества Мандельброта, когда преобразование фрагмента во все множество
нетривиально [7].
Изложив основные представления о предмете нашего
исследования, попытаемся сформулировать собственную концепцию относительно
понятия детерминированного хаоса. Прежде всего, несмотря на существующее мнение
[8] о невозможности дать фракталам точное определение, дадим его: фракталы –
это гиперкомплексные объекты нецелочисленной размерности пространства-времени с
пространственной или пространственно временной локализацией самоподобных
элементов в общей иерархической итеративной структуре.
По мнению Ю.А.Данилова и Д.Д.Кадомцева [9],
размерность объекта зависит от наблюдателя, точнее, от связи объекта с внешним
миром. Исходя из этого нами было доказано, что
размерность классического фрактала «снежинка Коха» с двумерной точки зрения
наблюдателя имеет фрактальную размерность, отличную от размерности Мандельброта
(d = ln4/ln3 » 1,2618) [10]. То есть доказано, что «снежинка Коха»
не является плоской кривой двумерной плоскости, а представляет собой
многослойную фрактальную конструкцию и ее топологическая размерность составляет
d = ln7/ln2 » 2,80735… С точки зрения трехмерного наблюдателя
топологическая размерность составит d = ln9/ln2 »
3,1699250, а при предельном стремлении итеративных операций поворота и фрактализации по алгоритму исходных фигур – двух
тетраэдров [11] фрактально заполняется элементарная кубическая ячейка
пространства [12]. Тем самым мы показали, что порядок лежит в основе
фрактальных структур изначально как алгоритмическая операция итерационного
построения их пространственно-временных конфигураций.
В серии статей [13]
обосновываются представления о пространственных конфигурациях и дифракционных
элементах на таких регулярных топологиях, как сложные структуры с
предсказуемыми детерминированными определениями порядка, за счет введения общей
классификации возможных принципов заполнения (выполнения) пространства с
помощью унифицированной обобщенной эйлеровой
характеристики – числа информационных осей симметрии.
Результатом всех упомянутых исследований явилось
построение общей физико-математической модели классификации многогранников и
оптимальных решеточных и полостных структур плотного и сверхплотного выполнения
пространства с использованием обобщенной эйлеровой
характеристики в следующей трактовке [14]:
![]() , (1)
, (1)
где d – топологическая размерность
характеристики; Т – число вершин; F – число граней; R –
число ребер многогранников.
При рассмотрении этой характеристики применительно к
правильным платоновым телам можно убедиться в
справедливости расширенной характеристики
![]() . (2)
. (2)
Не составляет труда убедиться, что эта характеристика
приводится к хорошо известной теореме Эйлера для многогранников
![]() . (3)
. (3)
Другими словами, введенная характеристика Nd справедлива для описания всех эйлеровых многогранников.
Обобщенная характеристика – число
информационных осей симметрии позволяет не только вычислить для любой
многогранной структуры известные из теории симметрии оси, но и перечислить также
направления (или оси) их естественного роста, т.е. простой трансформации
концентрического подобия [15].
С другой стороны, одним из
авторов настоящей статьи в ряде работ [16] для возможности гиперкомплексного
отображения различных пространственно-временных конфигураций во внешнее и
внутреннее пространство объектов и динамических процессов, присущих этим
объектам, был разработан математический аппарат геометрического поля
пространственных частот. Этот математический аппарат логически обоснован точным
решением задачи математических бильярдов в круге и векторных отображений
траекторий бильярдного шара во внешнее и внутреннее пространство «кругового
бильярда» (рис. 1).
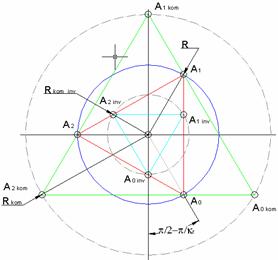
Рис 1. Многомерная модель гиперкомплексных
отображений
рациональной модовой траектории шара в круговом
бильярде
В настоящее время нами достаточно полно описаны траектории движения лучей многократного отражения в круге
(сфере) [18, 24, 27]. При этом установлено, что лучи света в отражающем круге образуют
траектории, форма которых зависит от коэффициентов фрактальности и полностью
ими обусловлена. Коэффициент фрактальности k определяет сектор круга g, который содержит в себе в качестве хорды длину
свободного пробега луча от одного отражения до другого отражения от
ограничивающей круговой поверхности
![]() . (4)
. (4)
При k целочисленных
траектории распространения лучей в круге статические и представляют собой
правильные вписанные в окружность многоугольники с числом вершин k.
В случае k
рациональных и определяемых отношением целых несократимых чисел
![]() (5)
(5)
траектории распространения света также
статические и представляют собой фрактальные многоугольники, т.е. правильные
звездчатые замкнутые многоугольники, имеющие n вершин. Они формируются
путем “заметания” лучом конечной площади в круге за m оборотов вокруг
центра кривизны.
При k трансцендентных траектории луча
динамические и луч “заметает” бесконечную площадь. Трансцендентные траектории
лучей – правильные незамкнутые звездчатые многоугольники с периодом,
равным бесконечности. В процессе формирования этих траекторий
точки текущих отражений никогда не вернутся в исходную точку первого
отражения и никогда не накладываются на окружности друг на друга. Другими
словами, можно утверждать, что при многократных отражениях от криволинейных
поверхностей отражения последняя (в нашем плоском случае – окружность)
выступает в качестве добавленной параметрической координаты. Ее заполнение
точками отражения подчиняется общим принципам «решета» Эратосфена,
аналитический вид которых был выведен одним из авторов этой статьи ранее [17].
Из этих определений следует, что порядок и хаос
связаны воедино как неотъемлемые элементы всех конструкций и динамических
структур пространства-времени. Само же пространство-время является фазовым
пространством, описываемым уравнениями геометрического поля пространственных
частот [18]. Вокруг и внутри любых пространственно-временных областей
формируется фазовая гиперкомплексная структура – структура разрешенных
информационных (фазовых) направлений отображения статической и динамической
конфигурации объектов. Эта структура в ранних работах Максвелла именовалась
эфиром («шестеренками» Максвелла»). В настоящее время данная парадигма развивается
в понятиях эфиродинамики [19].
Статическая структура фазового (геометрического) поля
пространственных частот обусловлена целочисленными или рациональными элементами
векторных отображений. Им соответствует распределение составных
рациональных чисел в числовом континууме. Закон этого распределения, как
уже отмечалось, выведен одним из авторов настоящей статьи [20].
Внутри структуры простых и составных
рациональных чисел числового континуума динамически распределены
трансцендентные числа. Они и составляют доминирующую часть мощности континуума.
Соединение элементов пространства-времени в сложные
статические и динамические системы порождает еще более сложное поле фазового
(геометрического) отображения всех пространственных форм и динамических
процессов системы во внешние и внутренние среды пространства-времени. В силу
того, что как для простых, так и для сложных элементов и систем
пространства-времени неотъемлемыми свойствами гиперкомплексного отображения
являются свойство самоподобия и самоорганизации коммуникаций
за счет детерминированно–хаотичного взаимодействия
векторных отображений, характеризуемых трансцендентными определителями
(коэффициентами) фрактальности, можно утверждать, что для любой сложной
динамической системы хаос и порядок являются неантогонистическим
единством их состояний.
Особое значение в объяснении этих процессов
приобретают понимание единства и внутренней перемежаемости
отображений пространств-времени
с разной природой формирования структур вещества (элементов), дополняющих общее
многомерное пространство-время.
Возможность создания веществ с правовращающей и
левовращающей тройкой векторов электромагнитного поля была предсказана еще в 70‑е
годы ХХ в. советским физиком В.Г.Веселаго, ранее выполнившим теоретическое
исследование свойств веществ с отрицательным n
[21]
Возможность распространения света в средах с
отрицательным показателем преломления [22]
![]() . (6)
. (6)
где
e0 и m0 – электрическая
и магнитная константы, не противоречит уравнениям Максвелла, но длительное
время не имела экспериментального подтверждения. В 2000 г. физиками из
Университета Калифорнии Р.Шелби, Дж.Смитом
и С.Шульцем [23] был синтезирован новый класс композитных материалов,
обладающих отрицательными электрической и магнитной проницаемостями в микроволновом
диапазоне. Создание левовращающих композитных материалов, построенных по нано-технологиям американскими и английскими
исследователями Д.Смитом, Р.Шелби, Дж.Пендри и др. [24] доказало
незыблемость электродинамики Маквелла для окружающего
нас пространства-времени.
В уравнениях геометрического
поля пространственных частот, дополняющих и объясняющих электродинамику
Максвелла в фазовом пространстве-времени [25], также найдена область значений
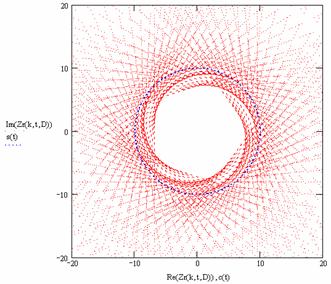
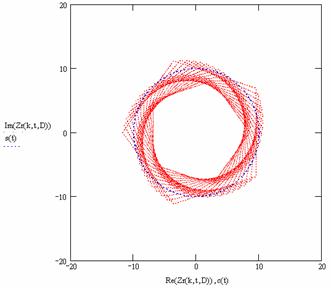
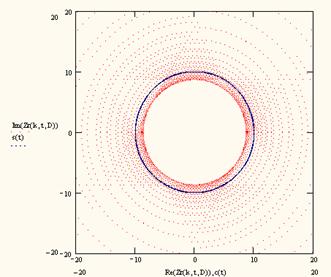
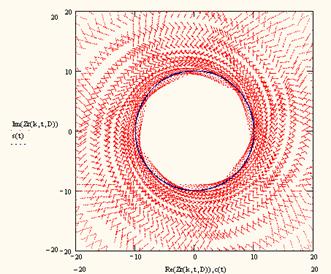
коэффициентов фрактальности k Î [0, ± 2], с помощью которой объясняются необычные процессы образования
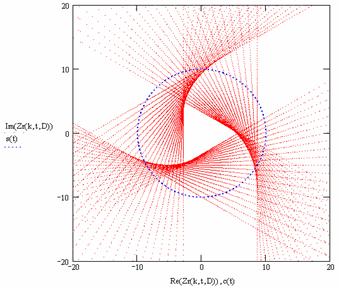
обратных волн отображения (табл. 1 а, б).
Таблица 1
|
k |
Отображение с D Î [–1, –0.9...1] |
|
3/2 |
|
|
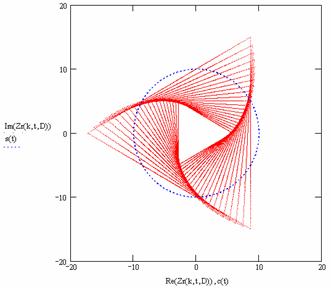
k |
Отображение с D Î [–1, –0.9...1] |
|
3 |
|
|
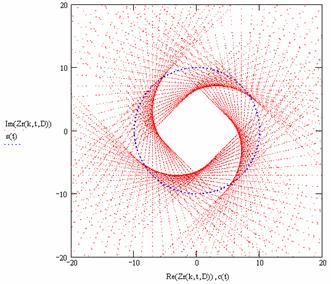
k |
Отображение с D Î [–1, –0.9...1] |
|
4/3 |
|
|
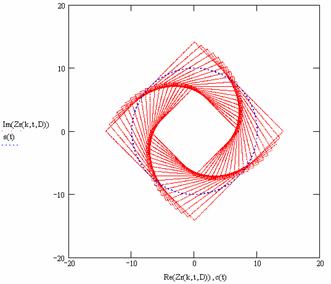
k |
Отображение с D Î [–1, –0.9...1] |
|
4 |
|
|
k |
Отображение с D Î [–1, –0.9...1] |
|
|
|
|
k |
Отображение с D Î [–1, –0.9...1] |
|
5 |
|
|
k |
Комплексное отображение траектории с k =
6/5 для левосторонних материалов (D Î [–1,
–0.9... 0]) |
|
6/5 |
|
|
k |
Изменение левостороннего комплексного отображения
траектории |
|
7/6 |
|
Результаты моделирования в программе Mathcad спиральных отображений правосторонних и
левосторонних векторов
Из таблицы 1 видно, что
– Диапазоны коэффициентов фрактальности k Î [2... µ] и k Î [–µ... –2] описывают распространение векторов геометрического поля
пространственных частот (соответственно правосторонних и левосторонних
относительно параксиальных векторов, для которых k = ½2½) при распространении потоков частиц в
“правосторонних” материалах.
– Диапазоны коэффициентов фрактальности k Î [0... 2] и k Î [–2... 0] описывают распространение векторов
геометрического поля пространственных частот (соответственно левосторонних и
правосторонних относительно параксиальных векторов, для которых k =
½0½) при распространении потоков частиц в “левосторонних”
материалах.
Доказательство
этих утверждений вытекает из анализа комплексных спирально-винтовых отображений
математических бильярдов в круге методами ГППЧ [26]:
· правосторонние векторы с коэффициентами фрактальности
от 2 до 6 комплексно отображаются во внешнее пространство в виде
закручивающихся вправо спиралей – правило правого винта для правосторонних
материалов;
· правосторонние векторы с коэффициентами фрактальности
от 6 до µ комплексно отображаются во
внутреннее пространство в виде закручивающихся влево спиралей – правило
левого винта для правосторонних материалов;
· левосторонние векторы с коэффициентами фрактальности
от 2 до 6/5 комплексно отображаются во внешнее пространство в виде
закручивающихся влево спиралей – правило левого винта для левосторонних
материалов;
· левосторонние векторы с коэффициентами фрактальности
от 6/5 до 0 комплексно отображаются во внешнее пространство в виде
закручивающихся вправо спиралей – правило правого винта для левосторонних
материалов. Подтверждение последнего утверждения представлено в табл. 1;
· как правосторонние, так и левосторонние векторы с
коэффициентами фрактальности, равными 6, отображаются на круге для
правосторонних материалов, а с коэффициентами фрактальности, равными
6/5, – на концентрических окружностях во внешнем пространстве для
левосторонних материалов (см. нижнюю строку табл. 1).
Первые
четыре из вышеприведенных выводов аналогично могут быть описаны и для
левосторонних (правосторонних) симметричных, относительно параксиальных (неспиновых) векторов, но со сменой винтовых ассоциаций на противоположные.
Интерес к
исследованию возможных аналогий композитных материалов с отрицательным
показателем преломления и графически синтезированных голограмм (дифракционных
элементов на графических транспарантах “Aires”) имеет вполне практическое
значение. В физико-математической модели [27] найдены частные описания целого
ряда регулярных и фрактальных структур плотной и сверхплотной упаковок
пространства. Показана также возможность вывода обобщенных уравнений. Примеры
простой кубической и сверхплотной кубической упаковок
сферическими симплексами приведены в табл. 2.
Таблица 2
|
Плотная упаковка пространства сферическими симплексами
по принципу простой кубической структуры |
|||
|
Объемный вид симплекса |
Сечение симплекса (плоскость, содержащая две
информационные оси |
||
|
|
|
||
|
Сверхплотная упаковка пространства сферическими симплексами
по принципу фрактализации абсолютного куба «Aires» |
|||
|
Сверхплотная суммарная кубическая упаковка симплекса |
Сверхплотная суммарная сферическая упаковка
симплекса |
Диагональное сечения сферической упаковки |
|
|
|
|
|
|
Моделирование плотной и
сверхплотной упаковок пространства
* * *
Возможность
управления процессами упорядочения хаоса, а соответственно и выявления
гносеологии детерминированного хаоса была установлена в ходе экспериментальных исследований,
проведенных сотрудниками ФРНМТ «Айрэс» и ГУП «ТКС-оптика», ГОИ. Было доказано, что постулируемые
положения о возможности связи структурных преобразований
решеток выполняемого физического пространства с решеточным пространством
тел арифметических прогрессий подтверждаются в полном объеме и позволяют
совершенствовать существующие матричные фрактальные топологии, показавшие
перспективу использования их в задачах нано-структурных технологий.
Предложенная трактовка природы детерминированного хаоса как прямое следствие
фрактальных свойств самого пространства-времени находит не только модельные
объяснения, но имеет также экспериментальные подтверждения.
* * *
Авторы выражают свою признательность А.А.Ошарину за оформление иллюстративных материалов и участие
в ряде экспериментальных исследований.
Примечания
1. Афанасьева В.В. Проблема динамического хаоса
в науке // Наука и культура. – Саратов, 2000. – С. 29–35.
2. Лоренц Э. Детерминированное непериодическое
движение // Странные аттракторы. – М., 1981. – С. 88–116.
3. Афанасьева В.В. Проблема динамического хаоса
в науке.
4. Лоскутов А.Ю., Михайлов А.С. Введение в
синергетику. – М.: Наука, 1990.
5. Афанасьева В.В. К философскому обоснованию
феномена детерминированного хаоса // Обзоры по электронной технике. –
1991. – Вып. 2.
6.
Mandelbrot B. Fractals: forms, chance and dimension. - San Francisco: W.H.
Freeman and Co., 1977; Id. The fractal geometry of
Nature. - San Francisco: W.H. Freeman
and Co., 1982.
7. Тарасенко В.В.
Метафизика фрактала (http://iph.ras.ru/~vtar/).
8. Там же.
9. Данилов Ю.А., Кадомцев Б.Б.
Нелинейные волны. Самоорганизация. – М.: Наука, 1983.
10.
11. Мельников Г.С, Серов И.Н. Задачи построения
геометрического волнового поля пространственных частот. – М.: Айрэс, 2001.
12. Мельников Г.С. Физико-математическая модель
решетчатых и шаровых упаковок пространства // Оптика и спектроскопия. (В печати. Рег. № 137 от 6.05.2003 г.).
13. Мельников Г.С. Физико-математическая модель
решетчатых и шаровых упаковок пространства; Он же. Математическая модель
классификации трансформаций многогранников с позиций минимизированной
обобщенной эйлеровой характеристики // Оптика и
спектроскопия. (В печати. Рег. № 133 от
6.05.2003 г.); Он же. Физико-математическая модель плотной
простой кубической упаковки пространства // Оптика и спектроскопия. (В печати. Рег. № 134 от 6.05.2003 г.); Он же. Вывод и
моделирование уравнений геометрического поля пространственных
частот // Оптика и спектроскопия. (В печати.
Рег. № 136 от 6.05.2003 г.); Мельников
Г.С., Ошарин А.А. Экспериментальное подтверждение
выводов по физико-математическому моделированию решетчатых и шаровых упаковок
пространства и моделированию уравнений геометрического поля пространственных
частот // (В печати. Рег. № 138 от 6.05.2003 г.); Они же. Математическое моделирование композитных материалов с отрицательным
показателем преломления и результаты предварительных экспериментальных
исследований на графически-синтезированных фрактальных топологиях // (В
печати. Рег. № 143 от 13.05.2003 г.); Мельников Г.С., Серов И.Н.,
Егорова Н.Б., Ошарин А.А. Физико-математическая
модель сверхплотной фрактальной упаковки пространства по топологии
«абсолютного» куба «Aires» // Оптика и спектроскопия. (В печати. Рег. № 135 от 6.05.2003 г.).
14. Мельников Г.С. Математическая модель
классификации трансформаций многогранников с позиций минимизированной
обобщенной эйлеровой характеристики.
15. Там же.
16. Мельников Г.С. Вывод и моделирование
уравнений геометрического поля пространственных частот; Он же. Теоретическое
исследование фокусировки излучения оптическим шаром методами аналитических
комплексных функций // Оптический журнал. (В печати. Рег.
№ 13561 от 17.01.2001 г.); Melnikov G.S. Gnoseology
of fractality – fractal optics // Proc.
SPIE. – 1997. – V. 3010. – P. 58–68.
17.
Melnikov G.S. Gnoseology
of fractality – fractal optics.
18. Мельников Г.С. Вывод и моделирование
уравнений геометрического поля пространственных частот.
19. Ацюковский В.А.
Концепции современного естествознания. – М.: МСЭУ, 2000.
20.
Melnikov G.S. Gnoseology
of fractality – fractal optics.
21. Веселаго В.Г. О свойствах веществ с
одновременно отрицательными значениями диэлектрической
(ε) и магнитной (μ) восприимчивостей // Физика твердого
тела. – 1966. – Т. 8, вып. 12. –
С. 3571; Он же. Электродинамика веществ с одновременно
отрицательными значениями ε и μ // Успехи физических
наук. – 1967. – Т. 92, вып.
№ 3. – С. 517; Веселаго В.Г., Глушков М.В., Рухадзе
А.А. // Физика твердого тела. – 1966. – Т. 8, вып. № 24; Веселаго В.Г., Рудашевский
Е.Г. // Физика твердого тела. – 1968. – Т. 8. –
С. 2862.
22. Рюэль Д., Такенс Ф. О природе турбулентности // Странные
аттракторы. – М.: Мир, 1981. – С. 117–151; Лоскутов А.Ю.,
Михайлов А.С. Введение в синергетику; Афанасьева В.В. К философскому
обоснованию феномена детерминированного хаоса.
23. Shelby R. A.,
Smith D. R., Schultz S. // Science. – 2001. – V. 292. – P. 77–79; Smith D.R.,
Schurig D., Pendry J.B.
Some of the waves emitted or reflected // Appl.
Phys. Lett. – 2002. – V. 81. – P. 2713–2715; Melnikov G.S., Serov
I.N. The use of fractal-matrix topologies in nanoscale
synthesis // Proc. SPIE by The IV International Symposium and Exbition “Photonics of Ukraine – 2003”. (In print); Мельников Г.С. Фрактальная
гносеология порядка и хаоса числового континуума и пространства-времени: Тез. докл.
на междунар. конф.
«Вероятностные идеи в науке и философии»; Мельников Г.С., Серов И.Н., Бычков
Э.В. и др. Сравнительный анализ простой кубической и сверхплотной
фрактальной упаковки пространства по топологии «абсолютного» куба
«Aires» // Тез. докл. на междунар.
конф. «Вероятностные идеи в науке и философии».
24. Pendry J.B. Negative refraction makes a
perfect lens // Physical Review Letters. – 2000. – V. 85, Is. 18. – P. 3966–3969; Pendry J.B., Holden
A.J., Robbins D.J., Stewart W.J. // IEEE Trans. Microwave
Theory Tech. – 1999. – V. 47. –
P. 2075–2084; Shelby R. A., Smith D. R.,
Schultz S. // Science. – 2001. – V. 292. – P. 77–79.
25. Мельников Г.С. Вывод и моделирование уравнений
геометрического поля пространственных частот.
26. Мельников Г.С., Ошарин
А.А. Математическое моделирование композитных материалов с отрицательным
показателем преломления…
27. Мельников Г.С. Физико-математическая модель
решетчатых и шаровых упаковок пространства; Он же. Математическая модель
классификации трансформаций многогранников…; Он же.
Физико-математическая модель плотной простой кубической упаковки пространства; Он
же. Вывод и моделирование уравнений геометрического поля пространственных
частот; Мельников Г.С., Ошарин А.А. Экспериментальное
подтверждение выводов…; Они же. Математическое моделирование композитных
материалов…; Мельников Г.С., Серов И.Н., Егорова Н.Б., Ошарин
А.А. Физико-математическая модель сверхплотной фрактальной упаковки пространства…
КМЗ им. Зверева, ОАО,
НПОС «ТКС-Оптика», ГОИ,
ФРНМТ «Айрэс»,
г. Сантк-Петербург
Dontsov, G.A., G.S.Melnikov and I.N.Serov. Fractal conception
of determined chaos
During the last few
years, the problem of classification and explanation of phenomena of determined
chaos is widely discussed in science and philosophy. In its turn, discovery of
determined chaos phenomena gave rise to new problems: how categories of order and
chaos now correlate? These and some adjacent problems are
considered in the paper.